from IPython.display import YouTubeVideo
YouTubeVideo('Vv3f0QNWvWQ')tl;dr: I hacked the emcee–The MCMC-Hammer ensemble sampler to work on PyMC models.
Motivation
PyMC is an awesome Python module to perform Bayesian inference. It allows for flexible model creation and has basic MCMC samplers like Metropolis-Hastings. The upcoming PyMC3 will feature much fancier samplers like Hamiltonian-Monte Carlo (HMC) that are all the rave these days. While those HMC samplers are very powerful for complex models with lots of dimensions, they also require gradient information of the posterior. AutoDiff (as part of Theano) makes this very easy for exponential family models.
However, in the real world of Big Science, we often do not have likelihoods from the exponential family. For example, the likelihood function of HDDM – our toolbox to do hierarchical Bayesian estimation of a decision making model often used in mathematical psychology – has an infinite sum and requires numerical integration which make it non-differentiable. In many other areas of science, likelihoods result from complex non-linear models that take a while to compute as described in this recent post on Andrew Gelman’s blog.
Largely separated from the hype around HMC that machine learners and statisticians love, astrophysicists have been solving this problems in other ways. Ensemble Samplers with Affine Invariance do not require gradient information but instead run many samplers (called “walkers” – Walking Dead, anyone?) in parallel to cover the space. With expensive likelihoods, having parallel sampling (something that’s not possible with HMC yet) is a game changer.
For a fun visual depiction of HMC vs Ensemble Samplers, see these two videos (make sure to crank your speakers to the max and dance as if the NSA wasn’t watching):
Hamiltonian Monte Carlo sampler
Affine Invariant Ensemble sampler
YouTubeVideo('yow7Ol88DRk')While PyMC does not have support for these Ensemble Samplers, there is emcee – The MCMC Hammer which implements it. emcee however only has the sampler, it currently lacks the model specification capabilities and probability distributions that PyMC offers. It is thus an obvious idea to try and combine the emcee sampler with the PyMC functionality for model building. This here is a very dirty hack that does just that.
import numpy as np
import emcee
import pymc as pm/usr/local/lib/python2.7/dist-packages/scikits/__init__.py:1: UserWarning: Module mpl_toolkits was already imported from None, but /usr/local/lib/python2.7/dist-packages is being added to sys.path
__import__('pkg_resources').declare_namespace(__name__)This is copy pasted from the bioessay_gelman.py example of PyMC.
from pymc import *
from numpy import ones, array
# Samples for each dose level
n = 5 * ones(4, dtype=int)
# Log-dose
dose = array([-.86, -.3, -.05, .73])
# Logit-linear model parameters
alpha = Normal('alpha', 0, 0.01)
beta = Normal('beta', 0, 0.01)
# Calculate probabilities of death
theta = Lambda('theta', lambda a=alpha, b=beta, d=dose: invlogit(a + b * d), plot=False)
# Data likelihood
deaths = Binomial(
'deaths',
n=n,
p=theta,
value=array([0,
1,
3,
5],
dtype=float),
observed=True)
# Calculate LD50
LD50 = Lambda('LD50', lambda a=alpha, b=beta: -a / b)Build and sample from the model the PyMC way to see that the outcome between the Metropolis-Hastings sampler and emcee are the same.
m = pm.MAP([alpha, beta, theta, deaths])
m.fit()
m = pm.MCMC(m)
m.sample(5000, burn=1000)
pm.Matplot.plot(m)[****************100%******************] 5000 of 5000 completePlotting alpha
Plotting beta
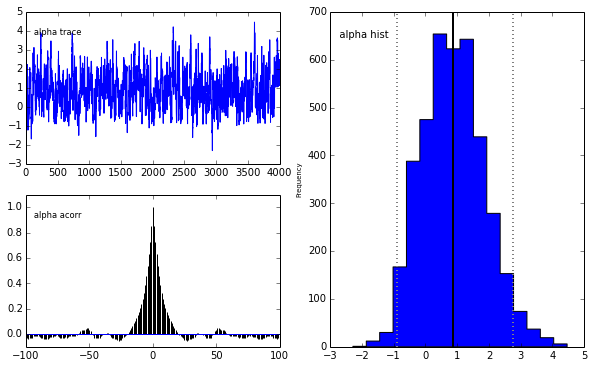
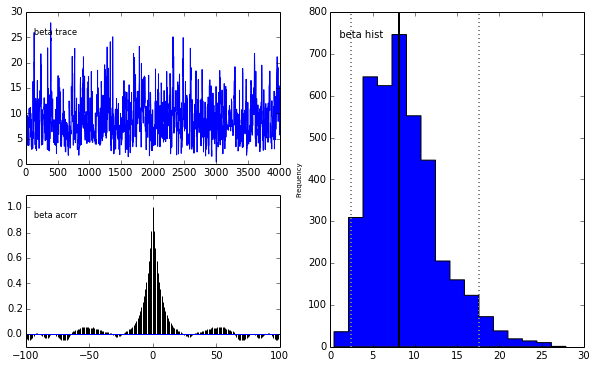
The unholy union
OK, you have been warned.
The central trick is to use the PyMC model to compute the logp of the model. We set the parameters externally and call .logp which we pass to the emcee sampler.
# Build model
m = pm.Model([alpha, beta, theta, deaths])
# This is the likelihood function for emcee
def lnprob(vals): # vals is a vector of parameter values to try
# Set each random variable of the pymc model to the value
# suggested by emcee
for val, var in zip(vals, m.stochastics):
var.value = val
# Calculate logp
return m.logp
# emcee parameters
ndim = len(m.stochastics)
nwalkers = 500
# Find MAP
pm.MAP(m).fit()
start = np.empty(ndim)
for i, var in enumerate(m.stochastics):
start[i] = var.value
# sample starting points for walkers around the MAP
p0 = np.random.randn(ndim * nwalkers).reshape((nwalkers, ndim)) + start
# instantiate sampler passing in the pymc likelihood function
sampler = emcee.EnsembleSampler(nwalkers, ndim, lnprob)
# burn-in
pos, prob, state = sampler.run_mcmc(p0, 10)
sampler.reset()
# sample 10 * 500 = 5000
sampler.run_mcmc(pos, 10)
# Save samples back to pymc model
m = pm.MCMC(m)
m.sample(1) # This call is to set up the chains
for i, var in enumerate(m.stochastics):
var.trace._trace[0] = sampler.flatchain[:, i]
pm.Matplot.plot(m)[ 0% ]Plotting alpha
Plotting beta
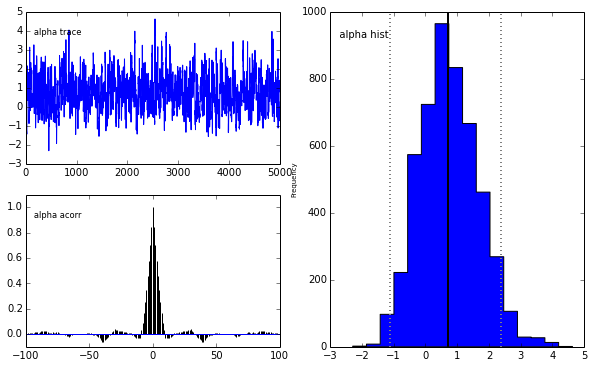
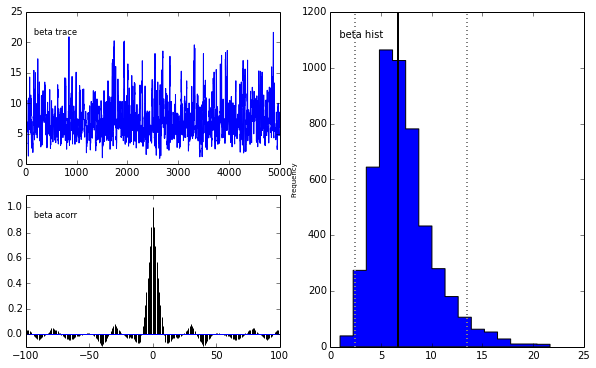
We get the same posterior back as with PyMC which is encouraging. The autocorrelation is also lower (with a high number of walkers, looks worse with fewer walkers) although I expected it to be even lower as this is a big selling point for emcee.
HMC vs Affine Invariant Ensemble samplers
I think HMC and Ensemble samplers are both relevant, albeit in different domains. Without having done any experiments, I expect HMC to do well for exponential family models with high dimensions and complex posteriors. Ensemble samplers can deal with non-differentiable, expensive to compute likelihood functions as they often appear in science. They can not escape the curse of dimensionality, however, as the size of the space grows exponentially but adding walkers only scales linear.
Future directions
emceecould be included intoPyMCas a custom step method which would reduce the hackiness.- Parallelization: For me the biggest selling point for Ensemble Samplers is that they can be parallelized quite easily (something not possible for HMC). This helps especially with expensive likelihoods that can require simulation to evaluate.
emceealready has support for this but thelnprobfunction must be pickable andPyMCmodels are not pickable. It is possible, however, to recreate aPyMCmodel in each process. This would be quite easy with this hack but doesn’t seem as straight forward ifemceewere integrated inPyMC.